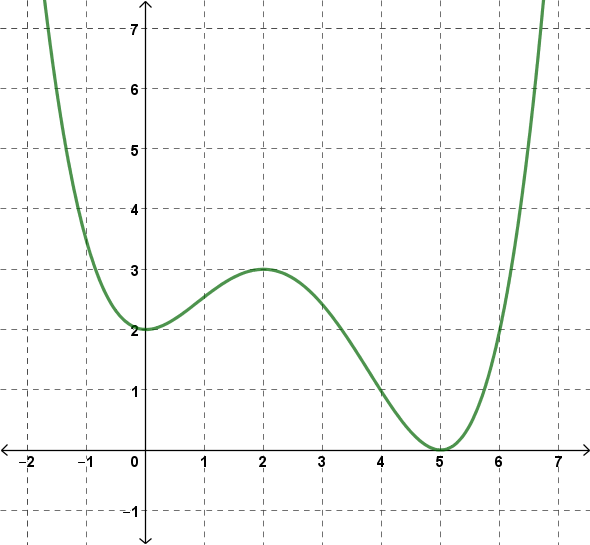
Gegeben ist der Graph einer Polynomfunktion f vom Grad 4 (siehe Abb.).

Aufgabenstellung: Berechne die Differenzenquotienten in den gegebenen Intervallen. 

[Wichtig: Gib Brüche als Dezimalzahlen an; Runde auf max. zwei Nachkommastellen. z.B. 1/2=0.5; 1/3=0.33]

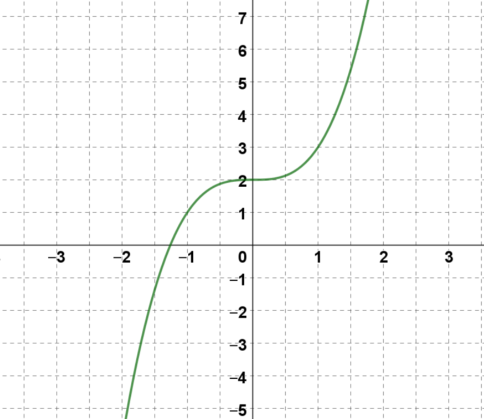
Gegeben ist der Graph einer Linearen Funktion f (siehe Abb.).

Aufgabenstellung: Lies aus der Graphik die folgenden Werte ab.

Gegeben ist die Funktionsgleichung einer Polynomfunktion vom Grad 4. f(x) = -1/200 x⁴ + 4x² - 400

Aufgabenstellung: Ermittle alle Extremstellen E₁, E₂ und E₃ der Funktion rechnerisch.

[Wichtig: Gib die Ergebnisse der Größe nach ein (E₁ < E₂ < E₃)!]

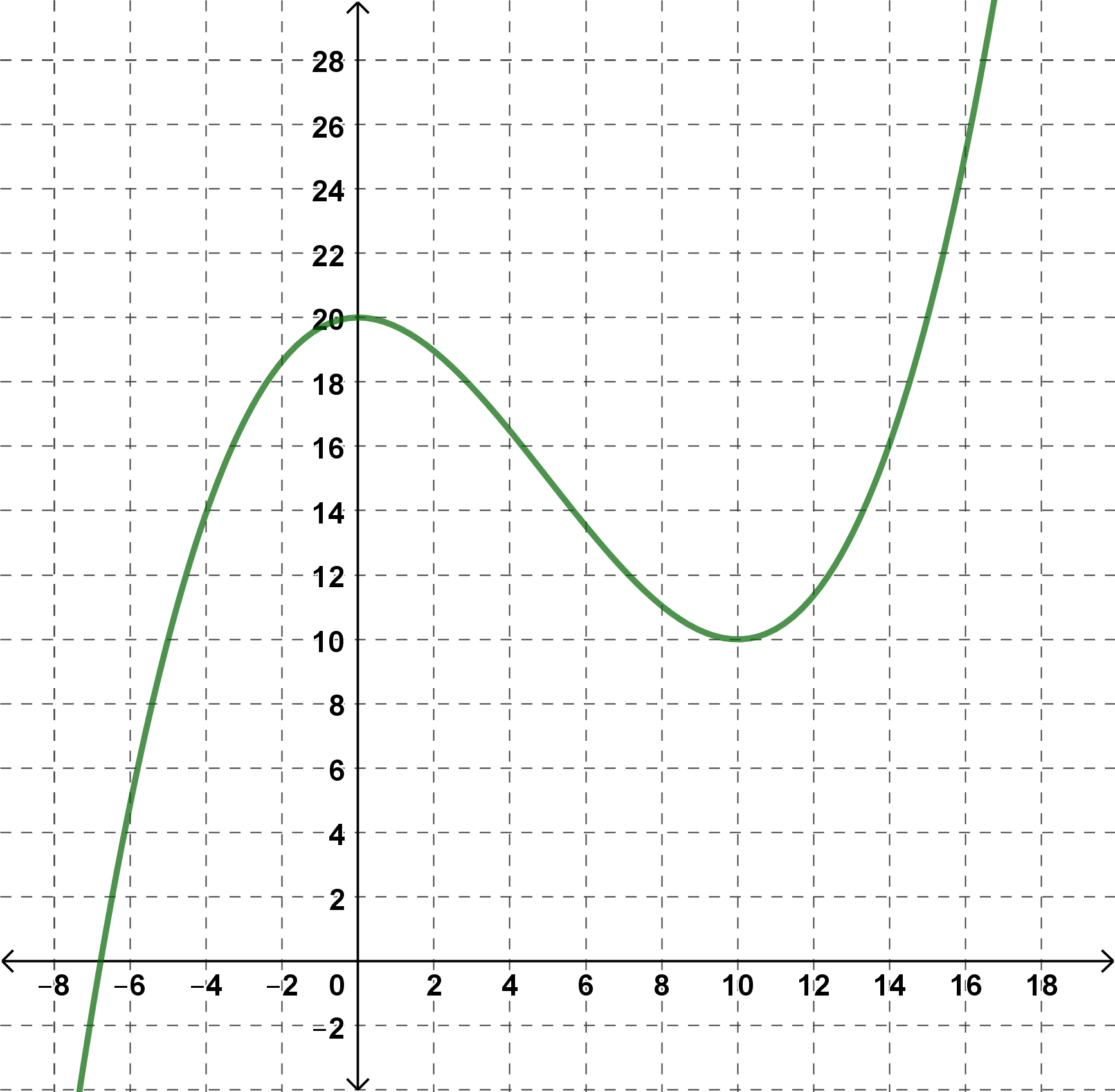
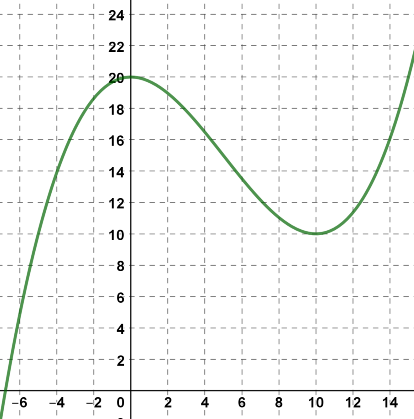
Gegeben ist der Graph einer Polynomfunktion vom Grad 3 (siehe Abb.).

Aufgabenstellung: Lies aus der Graphik die besonderen Stellen ab.

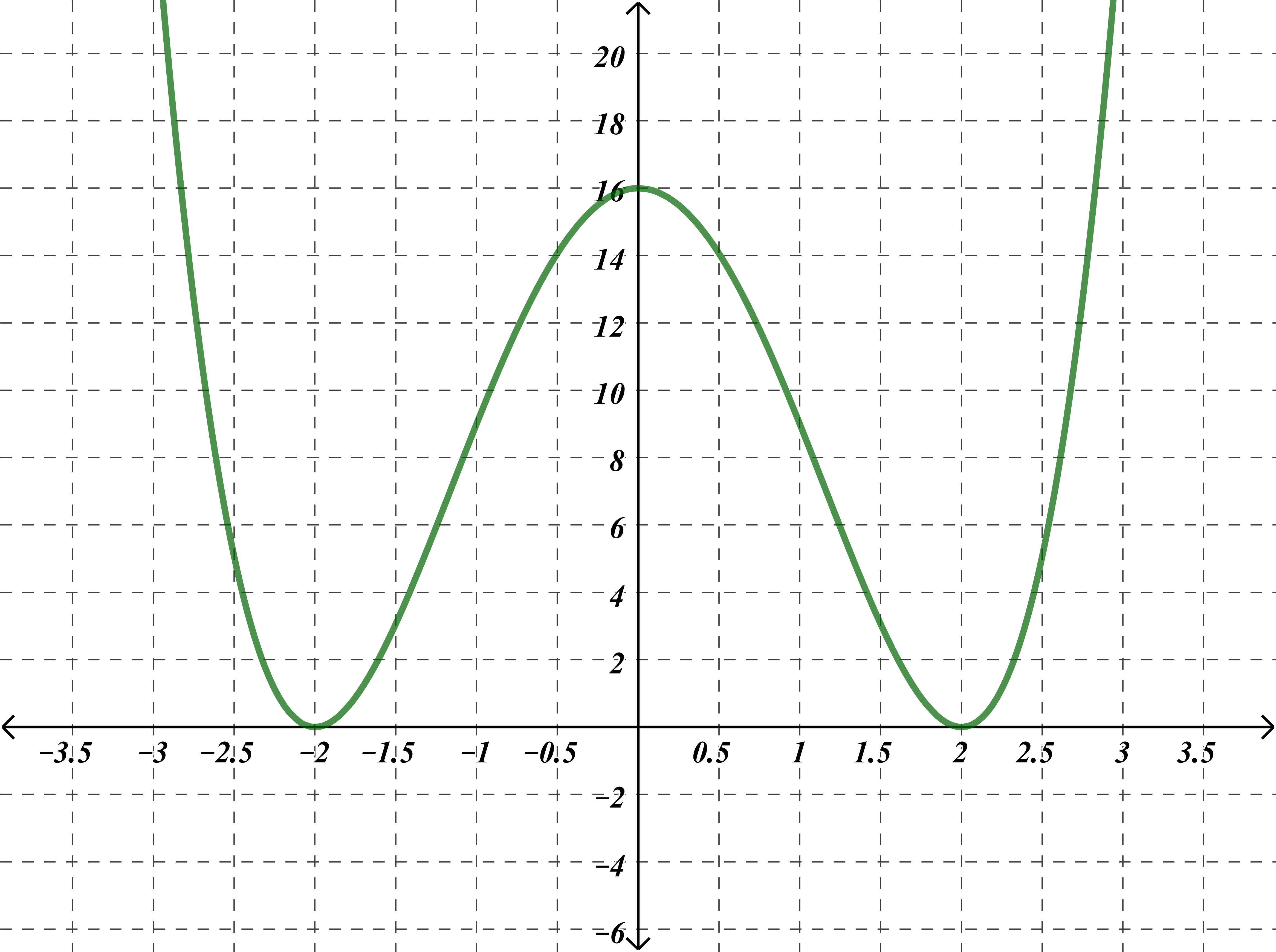
Gegeben ist der Funktionsgraph einer Polynomfunktion f vom Grad 4. Die Funktion ist achsensymmetrisch zur y-Achse.

Aufgabenstellung: Fülle in die Lücken jeweils die Zeichen <, >, = oder den gesuchten Zahlenwert ein. 

Gegeben ist der Funktionsgraph einer Polynomfunktion f vom Grad 3. Die Funktion ist punktsymmetrisch zum Ursprung.

Aufgabenstellung: Vervollständige die Aussagen mithilfe der Zeichen <, > und =.

Gegeben ist der Graph einer Polynomfunktion vom Grad 3 (siehe Abb.).

Aufgabenstellung: Lies aus der Graphik die besonderen Stellen ab.

Gegeben ist die Funktionsgleichung einer quadratischen Funktion f.

f(x) = -x² - 8x - 16

Aufgabenstellung: Ermittle die Scheitelstelle der Funktion rechnerisch. Gib außderm an, ob es sich dabei um ein Minimum oder ein Maximum handelt.